This is the first post of its kind on a computer science algorithm. For this example, we will consider a simple game and then see how the binary search algorithm works with it.

Let’s consider the “Guess the Number Game” first. A random number between 1 and 100 (not inclusive) will be chosen. The player will then have to guess the number. For example, if the random number is 50 and the player’s first guess is 75, the game would prompt the player that the desired number is between 1 and 75 – essentially the range where the random number do not fall in is discarded with each guess. The game then continues until the target number is correctly guessed.

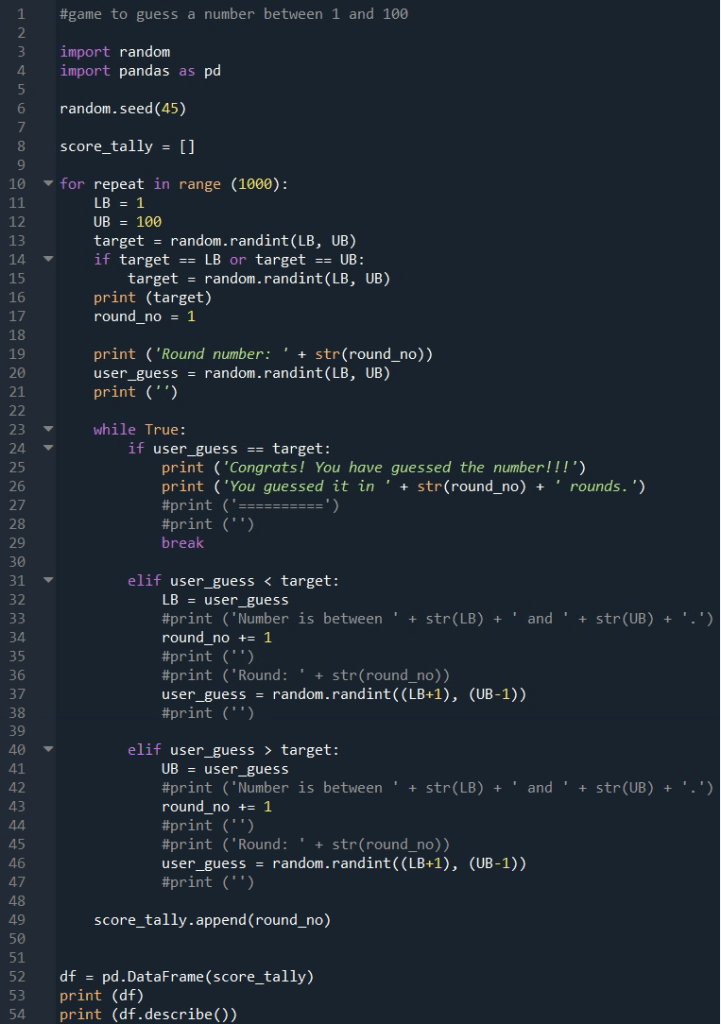
Let us consider the block of code below.

Line 1 imports the random module used to generate the target number.
Line 5 and 6 defines the lower and upper bound that will be used as the range to generate the random target number. Line 8 and 9 will select a different number should the random number happen to be 1 or 100.

Line 11 creates a variable that will track the number of rounds it take before the number is guessed correctly.
Line 14 will then store the player’s guess as a variable.

The remaining part of the code operates within a while loop, with three different if-else conditionals. Line 18 to 21 is the first condition where the player’s guess matches the target number.

For the nested conditional in Line 23 to 30, if the player’s guess is less than the target number, the player’s guess now becomes the lower bound limit. Similarly for the nested conditional in Line 32 to 39, if the player’s guess is more than the target number, the player’s guess now becomes the upper bound limit.

With the basic code of the game in place, we will modify it to play automatically, making random guesses for each turn. The number of rounds for each game is then logged as a list. A random seed value of 45 is used and 1000 games will be played using a for loop.

Some lines of the code have been commented out as we need not print the details of each round. Only the number of rounds of each game will be printed out on the IPython console. The list with the number of rounds taken for each game is then converted to a pandas dataframe, where the .describe() function is used to show the statistics of this set of game play.

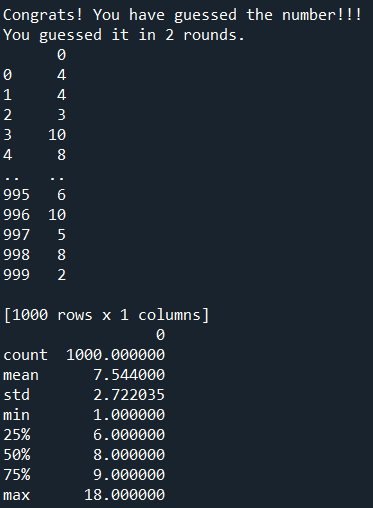
In the case of making random guesses, for this particular random seed value out of 1000 games, the minimum number of rounds is 1 (sheer luck…), while the maximum number of rounds is 18, with an average of around 7.54.

The following block of code then implements the binary search algorithm, where the guess will always be the middle value between the lower and upper bound values. A random seed value of 45 is also used.

In the case of using the binary search algorithm, for this particular random seed value out of 1000 games, we can see that the minimum number of rounds is still 1, but the maximum number of rounds has decreased to 7, with an average of around 5.79.

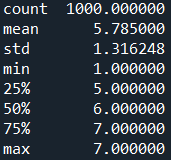
Thus the use of the binary search algorithm provides an improvement to the search performance required to find the randomly generated number within a given range.

Is there any way to make the above codes more concise and elegant? Feel free to comment.