I was trying out some Python problems on Codewars (www.codewars.com) when I came across this interesting problem titled ‘Blackjack Scorer’ posted by a user called ‘jodymgustafson’.

I find this problem interesting because there is a conditional involved when determining the value of an ‘Ace’ card, where it can either take a value of 1 or 11.

The code in this blog post is inspired by that problem, and it has been modified to allow the user to make a decision on whether to take the next card, and return the new value with each new card until the value exceeds 21 (i.e. busted).

Let us consider the block of code below. The code shown would not start from Line 1 or have continuous Line numbering as with previous post, as some comments/notes present in the code has been omitted for simplicity sake.

Line 10 imports the random module that will be used to randomly choose the initial two cards and the subsequent cards.

Line 12 to 25 defines a custom function which calculates the total value of the cards on hand. Line 13 replaces all ‘J’, ‘Q’ and ‘K’ to ’10’ and stores it in a new list variable using list comprehension. Line 14 counts the number of ‘A’ in this list, and Line 15 replaces all ‘A’ to ’11’.

Line 17 converts this list of strings to a list of integers. Line 21 to 23 is the algorithm that will decide whether an ‘A’ takes a value of 1 or 11; it uses a for loop to consider the number of ‘A’ and the total value currently, and changes the value that ‘A’ will take. The function then returns the total value as an integer.

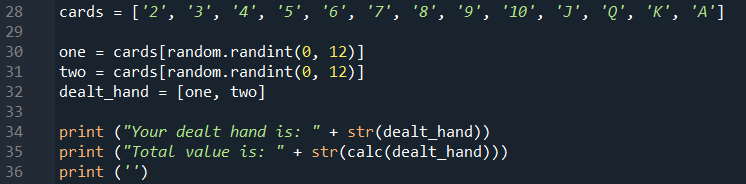
Line 28 creates a list of all possible cards. Line 30 and 31 chooses two cards at random for the starting hand, using a random number as the index for the list, and storing as a list in Line 32. Line 34 and 35 then prints this info in the IPython console.

In Line 38 and 39, if the starting hand has a value of 21, a ‘Blackjack!’ string will be displayed on the IPython console.

Line 41 to 56 uses a while loop, to allow the user to add new cards to the hand until the decision to stop, or when the total value exceeds 21. If the hand has a total of 5 cards and the value is still less than 21, the loop ends.

Line 42 asks for a user input to add a new card to the hand. If yes, a new card is randomly chosen from the cards list and added to the existing hand in Line 44, and the calc() function is called to re-calculate the new total value in Line 47. If no, the loop ends and the final total value is displayed, as determined in Line 52 to 56.

Note that this code does not take into account the probability of drawing any particular card.

Some screenshot of different runs of the code are shown below:

Is there any way to make the above codes more concise and elegant? Feel free to comment.

Disclaimer: The author of this post does not encourage or endorse gambling in any form. The coding logic behind counting the score for this example is pursued only for academic interest.