The travelling salesman problem asks the following question: “Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city and returns to the origin city?”

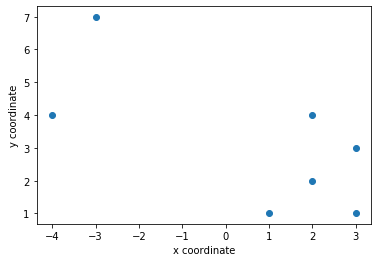
In the following post, the cities are represented by coordinates on a Cartesian plane. The distance (Euclidean distance) between any two points can be calculated using the Pythagoras Theorem. Using a series of for loops, the shortest possible distance, and the route, could be calculated. If the number of points (i.e. ‘cities’) are small, a brute force approach could be used. In this example, the seven points as shown below are used.

Let us consider the block of code below for creating an interactive data visual. The code shown would not start from Line 1 or have continuous Line numbering as with previous post, as some comments/notes present in the code has been omitted for simplicity sake. Nonetheless, some general comments are left in the code for reference.

Line 20 to 23 import the required modules for this example.
Line 26 to 28 create a function to calculate the distance between two points using the Pythagoras Theorem. This function accepts a total of four arguments in the form of the coordinates of the two points.
Line 31 to 37 assign the seven coordinate points. Line 39 stores these seven points as a list of tuples.

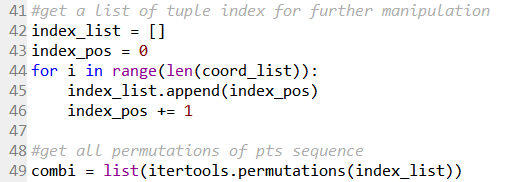
With a list of tuples, a separate list containing its indices is created. Line 42 first creates an empty list. Line 43 to 46 then populates this list with the respective number of indices. This will be the list that will be permuted, and the indices used to select the respective coordinates.

Line 49 creates another list with all the permutation sequences of the coordinates but rearranging the sequence of indices.

In the block of code shown below in Line 51 to 52, an empty array is created to store array of distances between the points for a given sequence of coordinates, while an empty list is created to store the respective sequence of coordinates.

Two nested for loops in a main for loop will be used to calculate the distance via a brute force approach. In Line 56, the main for loop will iterate for each permutation of the coordinate sequence. Line 54 and Line 90 will act as the counter for this loop.

In the first nested for loop from Line 59 to 64, each permutation is extracted from the list of list of tuples (combi) and stored in a temporary new_list.

An temporary empty array is created in Line 69 to store the list of distances between each sequential pair of coordinates.

The second nested for loop from Line 71 to 76 calculates the distances between each sequential pair of coordinates. Line 79 to 80 then calculates the distance between the last coordinate and the first coordinate. All calculated values are appended into the arr_of_dist array.

Line 84 sums the total distance. Line 85 then appends this value to the final_arr_of_dist array, which is defined outside the main loop, so it will consolidate all the total distance for each different permutation.

Line 86 does likewise to the corresponding permutation sequence, so that the total distance traveled can be matched to the respective coordinate sequence.

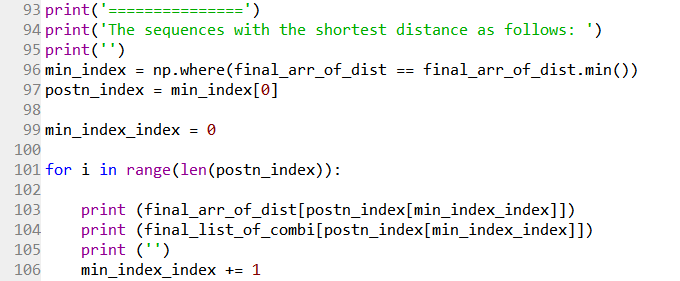
The next section of the code serves to identify the shortest distance traveled.

Line 96 uses the .min() method to find the minimum value in the final_arr_of_dist array. It will select repeated minimum values as well; this is essential as a different minimum value would have a different route taken. All the indices is stored as a tuple in the first element of the array as shown below. Thus, Line 97 isolates this tuple.

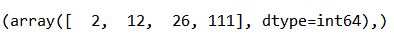
A for loop in Line 101 to 106 is then used to print out the shortest distances and their respective coordinate sequences. The output is as follows:

The following code from Line 109 to 114 first separate the list of tuples assigned to coord_list in Line 39 to two separate list using the unzip function (i.e. an inverse of zip, zip(*)), and plotted using the matplotlib module to generate the plot as shown at the beginning of this post.

There is something that could be improved with this code. The permuted sequence of 1-2-3-4 is deemed to be different to 4-3-2-1 using the itertools.permutation() method. However, these two sequences could be considered essentially the same, and they also give the same distance traveled. If one of the sequence in such a pair is removed, the computational time would be decreased when a larger set of coordinates is considered.

Is there any way to make the above codes more concise and elegant? Feel free to comment.